Electrical Power
Power is the rate at which work is done or energy changed from one form to
another and so:
Electrical Power = Energy/Time = VQ/t
Power = Potential difference (Volts) x Current (Amps)
Energy = Power x Time
Example problems
1. Calculate the power of a 12V light bulb using 2.5 A.
Power = VI = 12x2.5 = 30 W
2. Calculate the current used by a 12V immersion heater that is designed to deliver 30000J in 5 minutes.
Energy = Power x Time = 30000 Therefore 30000 = Power x 300 Power = 100W.
So current = 100/12 = 8.5 A
3. Calculate the energy given out by a 12V car battery that delivers a current of 200A for 3 s.
Energy = Power x time = VIt = 12 x 200 x 3 = 72 000 J
Two
alternative formulae for electrical power
We can combine Ohm's law with the basic formula
for electrical power to give two alternative formulae:
Since V = IR, and power = VI, we can
write
Electrical Power = VI = I2R = V2/R
Example problems
1. Calculate the resistance of a 100W light bulb if it takes a current of 0.8 A.
Power = I2R
Therefore R = 100/0.64 = 156.3 Ω
2. Calculate the power of a 12V immersion heater with a resistance of 10Ω.
Power = V2/R = 144/10 = 14.4 W
Problems
1. Calculate the power loss in an electrical transmission cable, 15 km long, carrying a current of 100A at a potential of 200 kV. The resistance per km of the cable is 0.2 Ω.
2. What power is supplied to the heater of an electric bar fire with
a resistance of 50 Ω connected to the mains 240V supply?
3. What is the power loss down a copper connecting lead 50cm long with a resistance of 0.005 W per metre when it carries a current of 1.5A?
Maximum power
transfer theorem
The external resistance will affect the current drawn from a source
of e.m.f, and therefore the energy lost within it since the same current will also flow through the
internal resistance. It is possible to find the value of this external resistance R that will give the
greatest power output.
In the circuit in Figure 1, consider the variation of the output power
of a supply of internal resistance with a load resistance R.
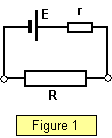
E = IR + Ir and so: EI = I
2R +
I
2r
Therefore: d(I
2R)/dR = EdI/dR – 2Ir dI/dr = 0 for a maximum.
Therefore E dI/dR = 2IdI/dR and so E = 2IR Therefore: E = 2IR = IR +
Ir
This therefore gives r = R for maximum power output and so the resistance of the load
should be equal to the internal resistance of the supply.
This is the case for an amplifier and
loudspeaker; the output impedance of the amplifier should be matched to that of the speaker. In
other words if the output impedance of the amplifier is 15Ω the resistance of the speaker should
also be 15Ω. However this condition is not necessarily the most efficient operating state of the
system.
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB


